Conclusion

At the state science fair, my project placed third.



These pictures were taken at the fair.



This is a format of my final layout.

Theoretical Review: Calculating Deviations

To calculate the speed of sound, I first used the formula d = 1/2*g*t^2:
I applied certain times, including 0, 0.5, 1, 1.5, and so on, also including 3.95, my measured time of fall. After this, I used an approximate measure of speed of sound (343 m/s), and divided each distance by that speed to get a variable which I subtracted from my original time to get a new time. I then applied this new time to my original formula, and reiterated this process, until the difference between two consecutive distances was negligible. Applying the final distance, I divide both the original distance, and the distance with speed of sound by the distance in meters between floors, and graph the answers.This graph shows the result.
It can be seen from this graph that the result is negligible and does not explain the difference between the projected and measured height of the building.

first drop video

Analysis of the video showed that the time of fall could be identified by looking at the audio signal. In this experiment it was 3.95 seconds. If the trash was fallung in a vacuum, this could be used to derive the height of the conduit.:
d = 1/2 * g * t^2 = 76 m.
I measured the distance between two adjacent floors as 2.58 meters. This makes the number of the floor from which the drop was done to be about 30. This is clearly not the case for the building I was using, which has a height of 18 floors (and the trash was dropped from the fifteenth floor), and therefore it took longer for the trash to fall than it would take if in a vacuum. I must repeat this experiment to confirm this result. If I receive similar results, conclusions about the nature of the fall in the trash conduit could be made.

Theoretical Review Part 5: The Exponential Function

This is an image I produced in Excel. It depicts two graphs; y = e^x, and y = e^-x. These two functions are important because they are used in my formula for velocity of the trash in the air.(See my previous post.) The first function, at x = 0, is equal to 1. As x increases, the function grows exponentially, because it is an exponent. The second function, since it is reciprocal, although starting with the same value of 1 at x = 0, decreases exponentially and by the time x reaches 3, for example, the value of the function falls approximately tenfold. This means that the value of the multiplicand in parentheses(basic formula of this experiment) will grow quickly.

Theoretical Review Part 4: Analysis of Trash Velocity

In the formula stating dependence of velocity "v" on time "t", v(t) = mg/b*(1-e^-bt/m), m is the mass of the trash,g is acceleration due to gravity, b is a constant proportional to the radius of the trash and the air viscosity(both will be considered constant), and e is the base of the natural logarithm, greater than 1. Consider the behavior of speed at different times: when time "t" is equal to zero, then mg/b will be multiplied by 1-e^0, which is one minus one which is zero.
Therefore, at the drop time, velocity will be zero, which is consistent with my experiment. When time becomes very large, mg/b will be multiplied by one minus the reciprocal of e to the power of a large number, with 0 as its limit. Therefore the multiplicand in the parentheses will be one, and therefore the velocity will be constant, and equal to mg/b. Since it is constant at large t, it is terminal velocity. This is also consistent.

Theoretical Review Part 3: Air Resistance

When an object is moving through the air, it experiences drag. Drag is a force that acts in the direction opposite to the object's movement and is proportional to the object's cross-sectional area and dependent on its speed(the more speed the more drag). It is instructive to look at how raindrops fall. In the beginning, we can assume that the speed of a raindrop towards the earth is zero. Acceleration, on the other hand, is equal to g. As the raindrop gains speed the drag increases, and the acceleration decreases. This means that the speed that the raindrop is gaining per second is decreasing. If the raindrop falls for a long period of time, at some point, it will reach a speed at which drag force is equal to gravitational force. Hence, its net force will be 0. It also means that it moves at constant speed. This is called terminal velocity. The estimation of drag force is complicated. It is known that besides being being dependent on the form of the object, it has a complicated dependence on the speed of the object. At low speeds, its value is proportional to the velocity of the object, and at high speeds, its value may become proportional to the square of the velocity of the object. It is believed that this switch in dependency occurs when the fluid around the object switches from viscous flow to turbulent flow. In the first approximation, it will be assumed that the trash in the trash chute moves in a viscous flow. The formula for the velocity of an object freely falling under the influence of gravitational force under viscous drag is




where m is the mass of the object, b is a constant dependent on the object's cross-sectional area and viscosity of the fluid.

In this project we will try to estimate the constant b from our experiments as an intermediary result.I will calculate a number of curves for a number of values of the b-constant. They are shown as curves on the above plot. The lower the curve, the bigger the cross-sectional area of the object. I, then, will drop the object from two floors: 15 and 7. These two drops will give me two times: t7 and t15. Knowing the distance between the seventh and fifteenth floor, I will find the curve on the above graph that describes the movement of the trash. This will be done by finding the curve the area under which between t7 and t15 is equal to the distance between the seventh and fifteenth floors. Knowing the curve will supply the absolute height of a given floor, as well as the value of the b-constant. From the latter, I will be able to estimate the viscosity of the fluid, using the following formula:

Theoretical Review Part 2

The acceleration due to gravity is approximately 9.8 meters divided by seconds squared:
g = 9.8m/s²      (1)

At any given time, the velocity of an object moving with gravitational acceleration is (gravitational) acceleration times travel time:

v = gt       (2)

where v is velocity at a given time, and t is time.

This follows from the definiton of acceleration.(a = v/t)

On a Cartesian v-t plane, the movement of an object moving at constant speed would look like this,

Since the area of a rectangle is height times length, which are measured velocity and measured time, the traveled distance is the area of the shaded rectangle.

The movement of an object with a constant acceleration would look like this:

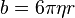
Using the formula for area of a triangle, we can determine that the distance is half of the measured time(base) times the measured velocity(height):

d = 1/2*t1*v1 (3)

Substituting (2) into (3), we get that distance is half of measured time multiplied by acceleration due to gravity multiplied by measured time:

d = 1/2*t1*g*t1

d = 1/2*g*t1^2      (4)

Using this formula, we can determine the height of the building by measuring the time.

To increase accuracy, we must also take into account air resistance and speed of sound.

Note. From formula (4) it follows that the measurement of the height of the building is linearly dependent on acceleration due to gravity. On time, however, it is quadratically dependant. This means that it is more important to know exact time than exact acceleration.

Theoretical Review Part 1

I will study the fall of trash in trash conduits in highrise buildings with the goal of determining the height of the building using the fall time.
The factors to be taken into account (in prioritized order) are acceleration/velocity due to gravity, air resistance that the trash is under influence of in the conduit, and speed of sound.
Speed of sound is taken into account to extract time needed for the sound signal to travel up the chute to the drop point.

Project Plan

Theoretical Review


Experiment


Experiment Analysis


Repeat Experiment(With New Parameters)


Final Conclusions


Science Fair Presentation


Science Fair