When an object is moving through the air, it experiences drag. Drag is a force that acts in the direction opposite to the object's movement and is proportional to the object's cross-sectional area and dependent on its speed(the more speed the more drag). It is instructive to look at how raindrops fall. In the beginning, we can assume that the speed of a raindrop towards the earth is zero. Acceleration, on the other hand, is equal to g. As the raindrop gains speed the drag increases, and the acceleration decreases. This means that the speed that the raindrop is gaining per second is decreasing. If the raindrop falls for a long period of time, at some point, it will reach a speed at which drag force is equal to gravitational force. Hence, its net force will be 0. It also means that it moves at constant speed. This is called terminal velocity. The estimation of drag force is complicated. It is known that besides being being dependent on the form of the object, it has a complicated dependence on the speed of the object. At low speeds, its value is proportional to the velocity of the object, and at high speeds, its value may become proportional to the square of the velocity of the object. It is believed that this switch in dependency occurs when the fluid around the object switches from viscous flow to turbulent flow. In the first approximation, it will be assumed that the trash in the trash chute moves in a viscous flow.
The formula for the velocity of an object freely falling under the influence of gravitational force under viscous drag is
where m is the mass of the object, b is a constant dependent on the object's cross-sectional area and viscosity of the fluid.
In this project we will try to estimate the constant b from our experiments as an intermediary result.
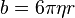
I will calculate a number of curves for a number of values of the b-constant. They are shown as curves on the above plot. The lower the curve, the bigger the cross-sectional area of the object. I, then, will drop the object from two floors: 15 and 7. These two drops will give me two times: t7 and t15. Knowing the distance between the seventh and fifteenth floor, I will find the curve on the above graph that describes the movement of the trash. This will be done by finding the curve the area under which between t7 and t15 is equal to the distance between the seventh and fifteenth floors. Knowing the curve will supply the absolute height of a given floor, as well as the value of the b-constant. From the latter, I will be able to estimate the viscosity of the fluid, using the
following formula:
I will calculate a number of curves for a number of values of the b-constant. They are shown as curves on the above plot. The lower the curve, the bigger the cross-sectional area of the object. I, then, will drop the object from two floors: 15 and 7. These two drops will give me two times: t7 and t15. Knowing the distance between the seventh and fifteenth floor, I will find the curve on the above graph that describes the movement of the trash. This will be done by finding the curve the area under which between t7 and t15 is equal to the distance between the seventh and fifteenth floors. Knowing the curve will supply the absolute height of a given floor, as well as the value of the b-constant. From the latter, I will be able to estimate the viscosity of the fluid, using the following formula: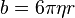
No comments:
Post a Comment